ВВЕДЕНИЕ

«… Математическое же искусство совершенно не принимает во внимание хорошее и дурное »

Аристотель

Математика – точная наука. Это очень важно в различных измерениях. Измерение – это сравнение с некоторым образцом (эталоном): метр, сантиметр, миллиметр, например [2;3]. Цель измерения (Приложение 2; 2) – установить, какое количество этих образцов можно поместить в измеряемом объекте. Эта количественная характеристика и является результатом измерения, а эталон становится единицей измерения.

В школьном курсе математики нам часто приходится измерять те или иные плоские фигуры. Они могут быть правильными и неправильными многоугольниками. Часто возникает необходимость найти площадь фигуры. (Приложение 2:1)

В жизни всегда необходимо уметь определять площадь различных поверхностей (Приложение 2; 3). Чтобы построить дом, необходимо правильно определить площадь земельного участка под строительство, площадь зелёных насаждений вокруг дома. При покупке мебели мы всегда учитываем площадь комнаты или кухни.

Измерение площадей необходимо во многих профессиях: в лёгкой промышленности, деревообрабатывающей, машиностроении. В сельском хозяйстве необходимо правильно определить площадь поля под посев, спланировать расходы посевного материала и ожидаемый урожай.

В задачах по геометрии часто требуется вычислить площадь многоугольника [1;337]. Решая задания ОГЭ по математике, мы рассматривали различные способы нахождения площади многоугольника на клетчатой бумаге, но, познакомившись с формулой Пика, стало значительно проще это делать.

Цель работы: изучить возможности применения формулы Пика при нахождении площади плоских многоугольников.

Задачи исследования:

- проверить эффективность и целесообразность применения формулы при решении задач;

- научиться применять формулу Пика в задачах разной сложности;

- сравнить задачи, решенные с помощью формулы Пика и традиционным способом.

Объектная область: комбинаторная геометрия.

Объектом исследования являются методы измерения площади фигур произвольной формы.

Предметом исследования является площадь фигур произвольной формы.

Методы исследования:

1. Изучение специальной литературы и Интернет-ресурсов.

2. Обобщение и систематизация материала по данной теме.

3. Отбор и анализ содержания источников информации;

Актуальность данного исследования состоит в том, что усвоение формулы может помочь школьникам, в том числе сдающим ЕГЭ, быстро и легко решать задачи на вычисление площади различных фигур на клетчатой бумаге.

Гипотеза: вычисление площади фигуры по формуле Пика обеспечит правильное и и быстрое решение задачи по сравнению с вычислением площади фигуры по формулам планиметрии.

Работа прошла следующие этапы.

1. Определение научного аппарата (определение цели, задач, методов исследования, гипотезы, актуальности).
2. Изучение методов вычисления площадей многоугольника на клетчатой бумаге.
3. Изучение источников (литературы, интернет-ресурсов).
4. Исследование методов решения:

- традиционного и с помощью формулы Пика;

- эксперимент;

- социологическое исследование.

Изучение источников показало следующее. Внимание к теореме Н.А.Пика возникло сразу же после его появления. Его использовали как математики, так и физики. Применялось решение с её использованием и в учебных заведениях разного уровня. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. Однако при изучении литературы, мы заметили, что она применима и в при нахождении площадей других фигур.

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо. Из литературы мы поняли, что такие или подобные им будут на ЕГЭ и ОГЭ. При помощи формулы Пика такие задачи решаются за минуту. Мы решили это проверить сами.

Для этого использовали различные сборники по ЕГЭ и ОГЭ, в том числе и интернет-ресурсы [5-8].

ГЛАВА I. ФОРМУЛА ПИКА И ЕЕ ПРИМЕНЕНИЕ

1.1.Историческая справка

Георг Алекса́ндр Пик (Приложение 1, фото 1) - австрийский математик, родился в еврейской семье. Годы его жизни 10 августа 1859 - 13 июля 1942.

Мать - Йозефа Шляйзингер, отец - Адольф Йозеф Пик.

Георг, который был одарённым ребёнком, обучался отцом, возглавлявшим частный институт. В 16 лет Георг окончил школу и поступил в Венский университет. В 20 лет получил право преподавать физику и математику.

Шестнадцатого апреля 1880 года под руководством Лео Кёнигсбергера Пик защитил докторскую диссертацию «О классе абелевых интегралов».

В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете.

Чтобы получить право чтения лекций, Георгу необходимо было пройти хабилитацию, то есть процедуру получения высшей академической квалификации, следующей после учёной степени доктора философии. Для этого он написал работу «Об интеграции гиперэллиптических дифференциалов логарифмами». Это произошло в 1882 году, вскоре после разделения Пражского университета на чешский (Карлов университет) и немецкий (Университет Карла-Фердинанда). Пик остался в Немецком университете.

В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом. Позже, в 1885 году, он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры.

Таким образом, мы видим, что Георг Александр Пик целенаправленно шел дорогой ученого, выбрав математику и физику. Именно это и дало ему возможность открыть формулу, которая получила его имя и используется при измерении площадей.

1.2. Доказательство

Формула Пи́ка (или теорема Пи́ка) - классический результат комбинаторной геометрии и геометрии чисел, согласно которому площадь многоугольника с целочисленными вершинами равна:

В + Г / 2 − 1, где В - количество целочисленных точек внутри многоугольника, а Г - количество целочисленных точек на границе многоугольника.

В частности, площадь треугольника с вершинами в узлах и не содержащего узлов ни внутри, ни на сторонах (кроме вершин), равна 1/2. Этот факт даёт геометрическое доказательство формулы для разницы подходящих дробей цепной дроби.

Доказана формула Георгом Пиком в 1899 году.

Вот это доказательство.

Пусть В – число узлов решетки, расположенных строго внутри многоугольника, Г – число узлов решетки, расположенных на его границе, включая вершины, — его площадь. Тогда справедлива формула Пика: S=В+Г/2-1.

Пример 1. Вычислить площадь многоугольника, изображенного на клетчатой бумаге по формуле Пика. S = В + Г/ 2 – 1

ДОКАЗАТЕЛЬСТВО размещены в полном варианте работы которая  размещена в ФАЙЛЫ по техническим причинам

Фундаментальный квадрат порождает решетку, то есть решетку можно построить следующим образом. Отметим вершины квадрата. Затем сдвинем его параллельно одной из его сторон на длину этой стороны и отметим две вновь полученные вершины. Если этот процесс продолжать сначала в одном направлении до длины a, а затем полученную полоску сдвинем параллельно себе в направлении другой стороны квадрата на длину этой стороны до длины b, то получим решетку.

Причем, число узлов решетки, лежащих внутри решетки, В = (а-1)(b-1), а число узлов решетки, расположенных на его границе, Г = 2a + 2b.

 Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник. Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

1.3. Вычисление площади кольца по формуле Пика

Возьмем кольцо, которое построим с помощью двух окружностей с радиусами R= 4 и r = 2.

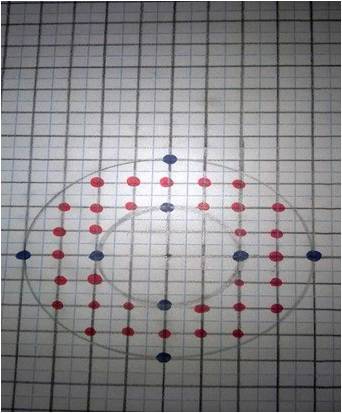
Вычислим площадь кольца с помощью формулы Пика:

В = 32, Г = 8, S= 32 + 4 - 1 = 35.

Вычислим площадь кольца по формуле площади круга, округлив число π до единиц.

S = πR² - πr² = 3* 16 - 3*4 = 48 - 12 = 36.

Округлим теперь π до десятых:

S = πR² - πr² = 3,1* 16 - 3,1*4 = 49,6 - 12,4 = 37,2.

А если округлить число π до сотых, то получим:

S = πR² - πr² = 3,14* 16 - 3,14*4 = 50, 24 - 12,56 = 37,68.

Сравнив результаты можно сделать вывод, что существует погрешность в вычислении площади по формуле Пика и, чем точнее число π, тем она больше.

Следовательно, данную формулу можно применять только для вычисления площадей многоугольников.

Таким образом, сделаем вывод. Находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов формула Пика работает хорошо.

Но надо помнить, что данную формулу можно применять только для вычисления площадей многоугольников.

ГЛАВА II. СРАВНЕНИЕ РЕШЕНИЙ

1. 1. Решение примеров.

Смотри ФАЙЛЫ

1. 2. Эксперимент

Нами был проведен эксперимент в 11-б классе (Приложение 4, эксперимент 1), в котором две группы одновременно решали одинаковые задание по вычислению площадей, но разными способами.

Это эксперимент доказал кратное уменьшение времени на решение с применением формулы Пика. Данный эксперимент нами был заснят на видео.

1. 3. Социологическое исследование

Так же было поведено социологическое исследование, в котором ученикам 9- а и 11-б классов предлагалось ответить на три вопроса.

1. Из каких источников вы впервые узнали о формуле Пика?
2. Будете ли вы применять формулу Пика при решении задач на нахождение площади?
3. Считаете ли вы, что для сдачи ОГЭ и ЕГЭ необходимы дополнительные знания по теории, которых нет в учебнике математики?

Результаты исследования отобразили в виде диаграмм (Приложение 3, диаграммы 1-2) и таблицы (Приложение 3, таблица 1).

Суммировав все варианты сравнения решений заданий с помощью формулы и традиционных способов, сделаем вывод, что они доказали преимущество использования формулы Пика.

ЗАКЛЮЧЕНИЕ

Существует бесконечное количество плоских фигур самой разной формы, как правильных, так и неправильных. Общее свойство всех фигур – любая из них обладает площадью (Приложение 2; 1).

Цель работы - изучить возможности применения формулы Пика при нахождении площади плоских многоугольников – достигнута.

Решены задачи исследования:

- проверена эффективность и целесообразность применения формулы при решении задач;

- научено применение формулы Пика в задачах разной сложности;

- задачи, решенные с помощью формулы Пика, и традиционным способом показали эффективность и упрощение решения.

Методы работы оказались эффективными. Наиболее интересными были эксперимент и социологическое исследование, которые доказали упрощение решения с помощью формулы Пика.

По итогу исследования мы сделали выводы:

1. Существует несколько способов нахождения площади многоугольника.
2. Нахождение площади по формуле Пика является самым простым и оптимальным для нахождения площади многоугольника на клетчатой бумаге.
3. Знания, полученные в ходе исследования можно легко применить для решения задач ЕГЭ и ОГЭ.

Несмотря на легкость самой формулы, она играет большую роль не только на экзаменах, но и в курсе математики, и даже на олимпиадах. Это очень полезная формула, что доказывает ее практическую ценность.

В ходе социологического исследования учащимся 9-г и 11-б были предложены вопросы. 1. Будете ли вы использовать формулу Пика на ОГЭ/ЕГЭ?. 96 процентов респондентов ответили утвердительно (Приложение 3, диаграмма 1)

Нами отобраны некоторые задачи для практического применения их при подготовки к ОГЭ. Они представлены в данной работе.

В ходе работы была изучена биография известного ученого, великого австрийского математика Г.А. Пика. Это расширило круг известных ученых с мировым именем.

Данная работа позволила формировать личные качества, такие как трудолюбие, ответственность, организованность, выдержка, которые необходимы в жизни.

Большое значение имеет возможность самоопределения в профессии, возможно, в будущем это будет способствовать выбору профессии, связанной с математикой.

ИСТОЧНИКИ

Литература:

1. Краткий справочник школьника.- М.: Дрофа, 1997
2. Я познаю мир. Детская энциклопедия. Математика.- М.: АСТ, 1998
3. 36 вариантов. Математика. Профильный уровень : типовые экзаменационные варианты . ЕГЭ. / под ред. И. В. Ященко. — М. : Национальное образование, 2018
4. 50 вариантов заданий. Математика. Профильный уровнень. ЕГЭ 2017/ И.В.Яшенко и др.- М.: Экзамен, 2016

Интернет ресурсы:

5. Инфоурок - https://infourok.ru/geometriya._metod_pika._vychislenie_ploschadi_figury-588021.htm
6. . Калькулятор - https://www.calc.ru/Kubicheskiye-Uravneniya-Formula-Pika.html
7. 5.Математика? Легко!!! - https://matematikalegko.ru/formuli/ploshhad-figury-na-liste-v-kletku-formula-pika.htm
8. Сайт Решу ЕГЭ - https://ege.sdamgia.ru/